
Aria dreptunghiului. Un dreptunghi este un patrulater cu patru unghiuri drepte. Poate fi definit și în alt mod: un paralelogram care conține un unghi drept – dacă un unghi este drept, celelalte trebuie să fie la fel. Mai mult, fiecare parte a unui dreptunghi are aceeași lungime cu cea opusă acestuia. De asemenea, are laturi adiacente inegale, spre deosebire de un pătrat.
Aria este o unitate de măsură a cât de mult spațiu există în interiorul unei forme. Calculul suprafeței unei forme sau a unei suprafețe poate fi util în viața de zi cu zi – de exemplu, poate fi necesar să știți cât de multă vopsea să cumpărați pentru a acoperi un perete sau cât de multă semințe de iarbă trebuie să semănați un gazon.
Pentru a găsi o valoare a unei arii trebuie să cunoaștem dimensiunea pe care o reprezintă un dreptunghi. Aria se aplică pentru orice unitate de lungime sau distanță. De exemplu, ați putea folosi centimetri, metri, mile, picioare etc. În matematică prescurtăm „centimetri pătrați” la cm², „2” înseamnă „pătrat”.
Cele mai simple (și cel mai frecvent utilizate) calcule de suprafață sunt pentru pătrate și dreptunghiuri.
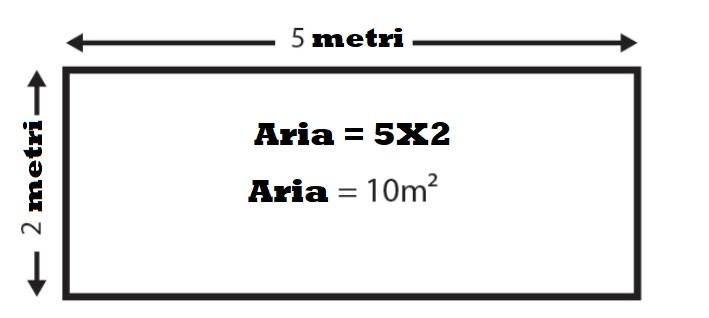
Pentru a găsi aria unui dreptunghi, se înmulțește lungimea cu lățimea.
Aria dreptunghi = L * l
Dreptunghiul are multe proprietăți interesante.
Intersecția diagonalelor este circumcentrul – există un cerc care are un centru în acel punct și trece prin cele patru colțuri. Într-un dreptunghi cu diferite lungimi laterale (pur și simplu vorbind – nu un pătrat), nu se poate desena cercul.
Liniile care unesc punctele medii ale laturilor unui dreptunghi formează un romb, care este jumătate din aria dreptunghiului. Laturile formei sunt paralele cu diagonalele.
În mod surprinzător, suntem înconjurați de obiecte dreptunghiulare. De aceea, calculul nostru poate fi util nu numai pentru cursurile de matematică, ci și pentru problemele din viața de zi cu zi. Desigur, nu vom găsi un dreptunghi ideal în realitate, deoarece are întotdeauna o a treia dimensiune; dar dacă este mică în comparație cu celelalte două măsurători, aproximarea este suficient de bună.