
Triunghi isoscel. Matematica este percepută ca fiind una dintre cele mai grele discipline învățate în școală. Cu toate acestea, sunt mulți elevi care au înclinații către această materie. Matematica este împărțită în două: algebră și geometrie. Matematica este considerată un limbaj universal, care stă la baza descifrării întregului ciclu al creației.
Potrivit definiției generale, un triunghi isoscel este triunghiul care are două laturi congruente (egale), iar cea de-a treia latură se numește bază. Vă prezentăm mai jos un triunghi isoscel, unde se poate vedea cum latura BC este baza triunghiului ABC, iar laturile congruente (de lungimi egale) sunt AB și AC: [AB]≡[AC].
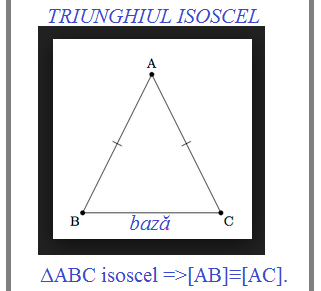
Termenul „isoscel” vine din greaca veche. Acesta a fost format din două cuvinte isos = egal și skelos = picior. Termenul s-a folosit în geometrie pentru denumirea triunghiurilor isoscele, deci în cazul în care două laturi (considerate ca fiind „picioarele” care se sprijină pe bază) ale triunghiului dat sunt egale.
Cine nu a auzit de teorema lui Pitagora sau cea a lui Thales? Cine nu a folosit aceste teoreme în ample calcule matematice? Ei bine, da, aceste teoreme sunt supercunoscute și vin în ajutorul celor care au de rezolvat probleme de matematică. Totuși, puțini sunt cei care știu că există și teorema lui Pompeiu, un cunoscut matematician român.
Într-o scurtă lucrare publicată în anul 1929, Pompeiu demonstrează că dacă integrala dublă a unei funcții continue în plan are aceeași valoare pe orice pătrat de latură dată, atunci funcția se reduce la o constantă. Aceasta simplă observație a generat una dintre cele mai interesante probleme ale analizei matematice, cunoscută sub denumirea de „problema lui Pompeiu”. În geometrie, teorema lui Pompeiu este următoarea afirmație: Fie triunghiul echilateral ABC, P un punct al planului ce nu aparține cercului circumscris triunghiului ABC. Atunci PA, PB, PC sunt lungimile laturilor unui triunghi.
Cea mai cunoscută teoremă a sa este teorema care-i poartă numele. În geometrie, teorema lui Pompeiu este următoarea afirmație: Fie triunghiul echilateral ABC, P un punct al planului ce nu aparține cercului circumscris triunghiului ABC. Atunci PA, PB, PC sunt lungimile laturilor unui triunghi. Teorema a fost descoperită în anul 1936 cu ajutorul numerelor complexe.
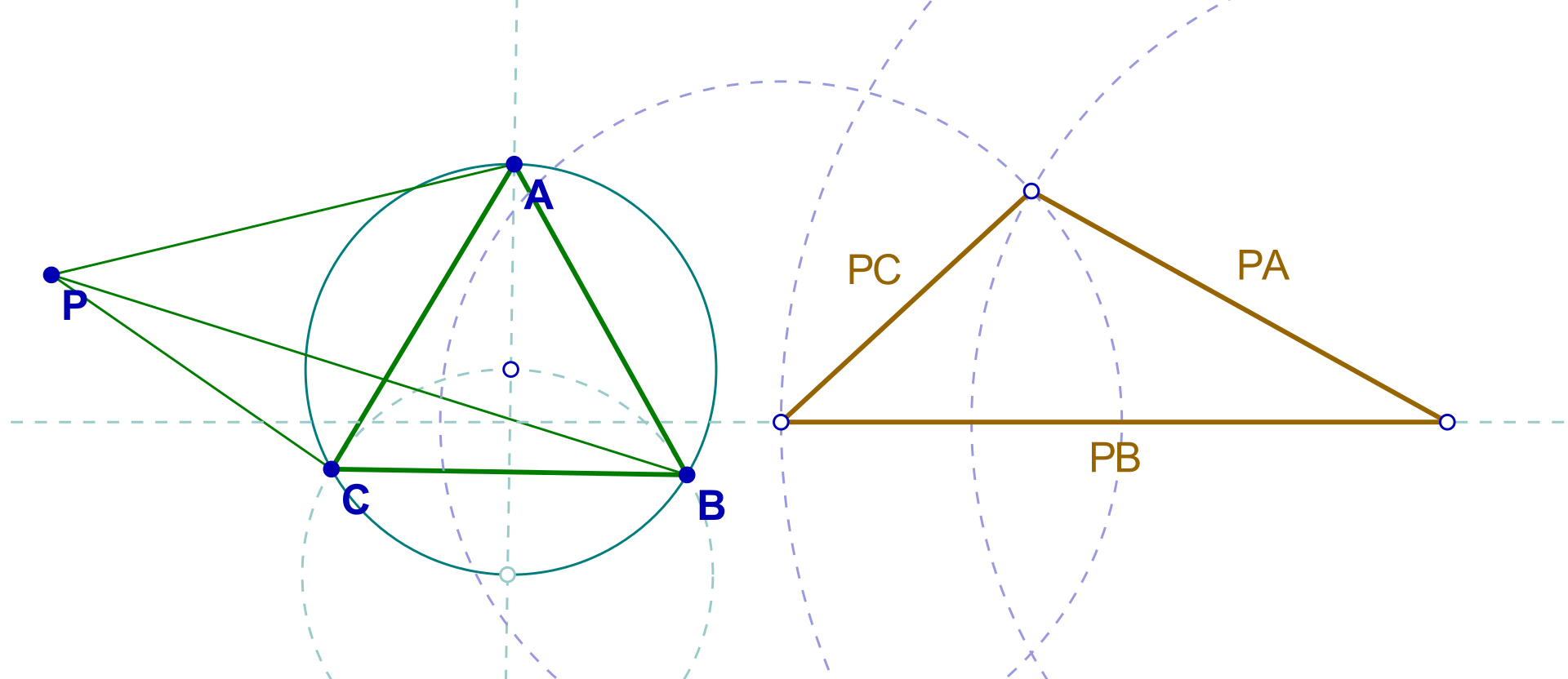
Foto: Pexels.com