
Teorema bisectoarei afirmă că într-un triunghi, bisectoarea unghiului interior împarte acest unghi în două unghiuri congruente, având mărimi egale ale laturilor opuse.
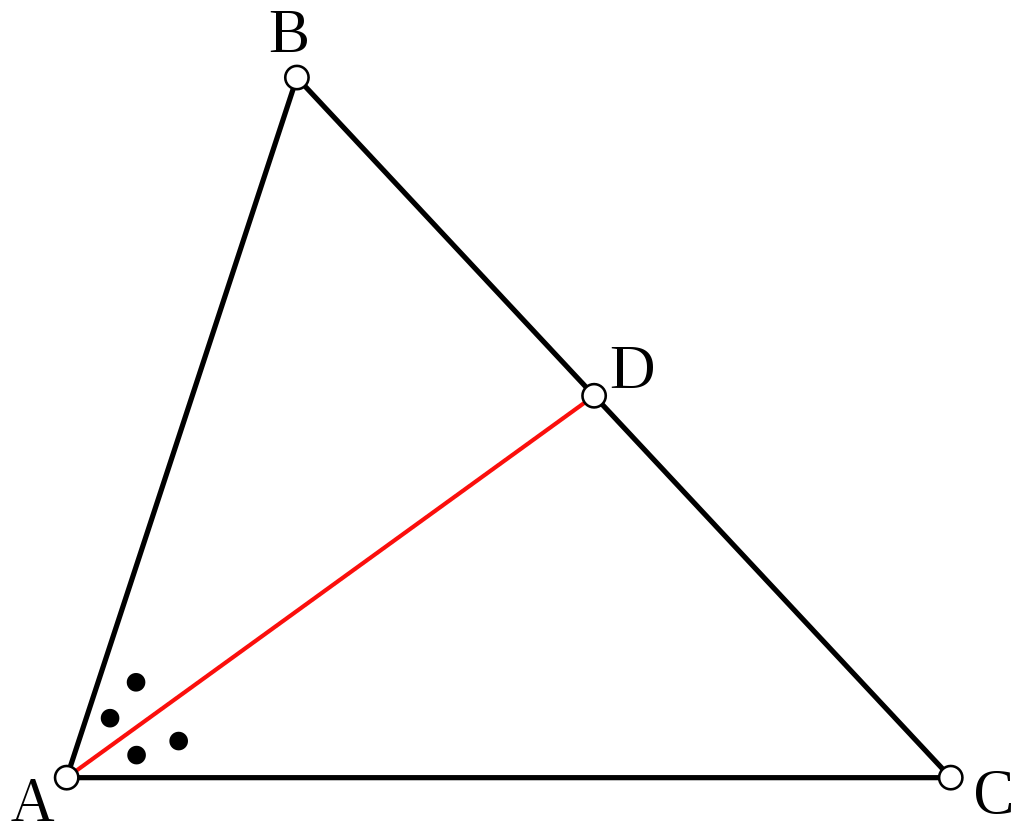
Mai precis, dacă în triunghiul ABC se trasează bisectoarea unghiului ∠BAC, iar aceasta intersectează latura BC în punctul D, atunci avem:
BD/DC = AB/AC adică raportul dintre lungimile segmentelor BD și DC este egal cu raportul dintre lungimile laturilor AB și AC ale triunghiului ABC.
Această teoremă are mai multe aplicații în geometrie și este folosită, printre altele, pentru a găsi lungimea unei laturi a triunghiului dacă cunoaștem lungimile celorlalte două laturi și măsura unghiului opus celei de-a treia laturi.
Reciproca teoremei bisectoarei: Dacă un punct D interior laturii BC o împarte pe aceasta în segmente ce respectă relația
, atunci AD este bisectoarea unghiului A.
Bisectoarea unui unghi este semidreapta cu originea în vârful unghiului, care împarte acest unghi în alte două unghiuri de măsuri egale.
Orice punct de pe bisectoare se află la egală distanță de laturile unghiului, proprietate pe baza definiției bisectoarei.