
Când privim în jur, observăm o multitudine de numere: de la etichetele produselor, la măsurarea temperaturilor sau la calcularea distanțelor. În acest univers al numerelor, o categorie esențială este reprezentată de numerele reale. Acestea sunt, de fapt, o extindere a numerelor cu care suntem deja familiarizați: întregi, fracții, zecimale. Dar ce sunt aceste numere reale și de ce sunt atât de speciale? Haideți să descoperim împreună!
Cu mii de ani în urmă, matematicienii antici se confruntau cu o problemă: cum să reprezinte și să calculeze lungimile care nu pot fi exprimate ca fracții simple? Aceasta a fost începutul călătoriei către descoperirea numerelor iraționale și, ulterior, a conceptului de număr real. De-a lungul timpului, matematicienii precum Pitagora, Euclid sau Cantor au contribuit la evoluția și înțelegerea acestui concept.
Orice număr care poate fi exprimat ca o fracție a două numere întregi este un număr rațional. De exemplu, 3443, 0,75 sau 1 sunt numere raționale. Un fapt interesant? Toate numerele zecimale care se repetă (cum ar fi 0,666…) sau care se termină (cum ar fi 0,25) sunt raționale.
Acestea sunt numerele care nu pot fi exprimate ca fracție a două numere întregi. Unul dintre cele mai cunoscute astfel de numere este √2, dar și numărul π. Zecimalele lor nu se repetă și nu se termină niciodată!
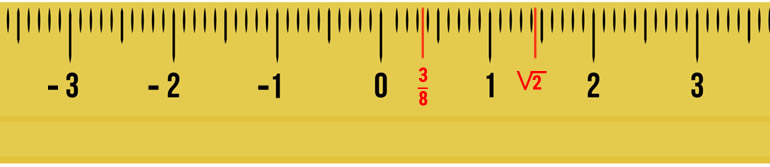
Axa numerică este o linie dreaptă pe care fiecare punct reprezintă un număr real. Numerele raționale și iraționale pot fi reprezentate pe această axă. De exemplu, imaginează-ți axa numerică ca o riglă infinită. Numărul 1 este la un centimetru, 2 la doi centimetri și așa mai departe. Dar și numerele dintre aceste mărci, cum ar fi ⅜ sau √2, au și ele un loc pe această riglă!
Operarea cu numere reale este similară cu operarea cu numerele pe care le știi deja. Dacă ai două numere reale, le poți aduna sau scădea la fel cum ai face cu două numere întregi sau zecimale.
Înmulțirea și împărțirea numerelor reale urmează și ele reguli similare. Trebuie doar să avem grijă atunci când înmulțim sau împărțim cu numere negative.
Așa cum întregii au anumite proprietăți (de exemplu, a + b = b + a), la fel au și numerele reale. Aceste proprietăți sunt esențiale în matematică și ne ajută să rezolvăm diverse probleme.
De la măsurarea lungimilor în construcții, la calculul vitezelor în fizică sau la determinarea prețurilor în economie, numerele reale sunt omniprezente. Ele sunt instrumentul matematicianului, fizicianului, inginerului sau economistului și ne ajută să înțelegem și să descriem lumea înconjurătoare.
Numerele reale sunt ca atomii în universul matematicii: mici, dar esențiale. Ele construiesc, descriu și definesc multe din fenomenele și problemele cu care ne confruntăm în viața de zi cu zi. Prin înțelegerea lor, ne deschidem ușile către o lume plină de posibilități și descoperiri.
Bibliografie Recomandată
Centimeter Vectors by Vecteezy